CFI60 infinity optics
Designed
to correct chromatic aberrations over the entire field of view, CFI60 objectives
produce images that are extremely sharp, of high contrast and have minimum
of flare. Furthermore, their 60mm parafocal distance and larger objective
diameter provide both longer working distances and higher numerical apertures.
Longer working distances are particularly useful when inspecting thick
samples.
Introduction
When typical microscopist speaks about Infinity Optics, they probably have
this image
of a dream optical system that can do anything. Some say performance increases
when you use a microscope with an infinity optical system. So they conclude
that if
it's not an infinity optical system, it is not performing at a high level.
Are all manufacturers really trying hard to make this happen and to meet
the
expectations of users? Is it true that infinity optics significantly improve
system
flexibility, but is infinity optical performance always superior to finite
optical systems?
Nikon CFI60 optical design team faced this proposition head on. They thoroughly
studied the advantages and disadvantages of other manufacturers' systems,
and found
an optimum balance between optical performance and system flexibility.
This
document will help you understand why an infinity optical system, for biological
applications, sets new performance standards incorporating a tube lens
with a focal
length of 200 millimeters, an objective with a parfocal distance of 60
millimeters, and
an objective thread size of 25 millimeters.
Why is the Focal Length of the Tube Lens 200 millimeters?
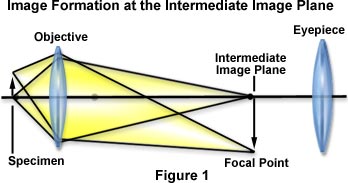
In a finite optical system, after light from an object passes through the
objective, it is
directed toward the primary image plane (often referred to as the intermediate
image
plane, located at the eyepiece focal point) and converges there as illustrated
in Figure
1.
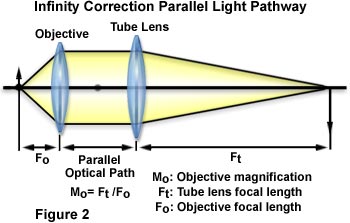
In an infinity optical system, however, light becomes a flux of parallel
rays after
passing through the objective and does not converge until after passing
through the
tube lens as shown in Figure 2. This does not mean that an infinite distance
can be
obtained after light passes the objective (up to the tube lens). After
passing through
the objective, light from an object on the optical axis moves parallel
to this axis along
the optical path. Light coming from the periphery of the object forms a
flux of parallel
rays and advances at a diagonal angle to the optical axis as diagrammed
in Figure 3,
presented below.
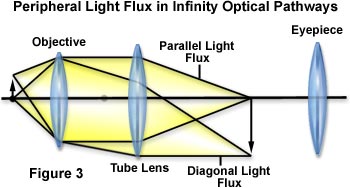
Because of this, there are instances where these rays of light can no longer
be
captured by the tube lens if the location of the tube lens is too far from
the objective.
This causes the image around the edges of the field of view to become dark
or blurred,
preventing the microscope from performing at its full potential. The term
Infinity Optics
simply means that light becomes a flux of parallel rays after passing through
the
objective, not that an infinite space is available inside the optical system.
If we are going to adopt infinity optics in order to further develop the
microscope, we
will need to increase the distance between the objective and tube lenses
as well as
increase the system flexibility. To lengthen this distance, we reduced
the angle of the
flux of parallel rays outside the optical axis. It is generally thought
that a longer focal
length for the tube lens will accomplish that, but this length has limitations.
The magnification (M(o)) of the objective in an infinity optics microscope
is obtained
using the formula:
Mo = tube lens focal length (Ft) / objective focal length (Fo)
where the tube lens focal length (F(t)) and objective focal length (F(o))
are described in
Figure 2. If the focal length of the tube lens is lengthened, the distance
to the image
plane (at the eyepiece) will also increase with the longer focal length
of the objective.
Naturally, this makes the size of the microscope larger. With this in mind,
the
conclusion reached was that a focal length of 200 millimeters would be
the most
appropriate for the tube lens. The focal lengths adopted by other manufacturers
are
160 millimeters and 180 millimeters.
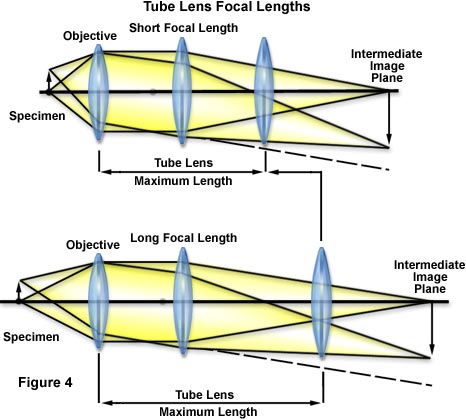
To obtain a same-size image from an object located far from the optical
axis, the
longer focal length of the tube lens produces a smaller angle of light
against the optical
axis. The light rays do not spread out so the distance between the tube
lens and the
objective can be increased greatly enhancing the potential for system flexibility
as
illustrated in Figure 4 below.
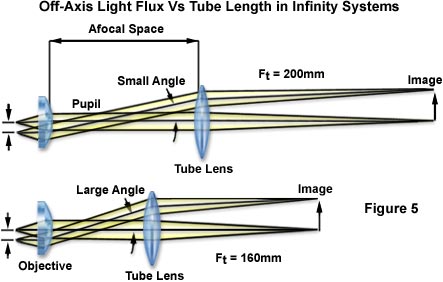
This design has certain optical advantages. As shown in Figure 5, when
tube lenses of
160 millimeters and 200 millimeters focal lengths are compared, the 200
millimeters
lens produces a flux of off-axis light rays with a smaller angle. In this
context, light
rays passing through the phase ring in a phase contrast attachment, the
DIC prism in
a Nomarski DIC attachment, or the dichroic mirror in an epi-fluorescence
attachment,
produce smaller shifts between light elements parallel to the optical axis
and those
diagonal to it, so that accessories work more efficiently. This is a big
optical
advantage, and also a primary factor contributing to an improved level
of contrast in
epi-fluorescence microscopy.
Why is the Parfocal Distance of the Objective 60 millimeters?
Once the tube lens focal length was set to 200 millimeters, the parfocal
distance of the
objective has to be increased from the standard 45 millimeters. As explained
in the
section on tube length, the focal length of the objective is also increased
in order to
preserve the same magnification, and since 45 millimeters does not provide
optimum
space in this design, a high-quality image cannot be obtained. In practice,
the CF N
Plan Apo 60x oil with a mechanical tube length of 160 millimeters, believed
to be the
ultimate in finite objectives, is crowded with lenses in a limited space
of 45 millimeters.
When this finite system is replaced with an infinite system and the objective
is divided
into an objective and a tube lens, the focal length of the tube lens becomes
the
equivalent of approximately 150 millimeters. On this basis, we can calculate
the
parfocal distance to provide an optical performance which surpasses that
of the finite
system as follows: The finite system objective parfocal distance is 45
millimeters; for a
tube lens focal length of 150 millimeters, the infinite system objective
parfocal distance
is x; and the tube lens focal length is 200 millimeters. In solving this
proportion, if 45 :
150 = x : 200, then x = 60 millimeters. Therefore, if the tube lens focal
length is 200
millimeters, the optimum objective parfocal distance has to be 60 millimeters.
Using the calculations above the optimum parfocal distance for a tube length
of 160
millimeters is 48 millimeters and for a tube length of 180 millimeters
is 54 millimeters.
For microscope manufacturers who set the objective parfocal distance in
their infinity
optics systems to 45 millimeters, then they are unable to exploit the full
potential of
their objectives.
Since the working distance (WD) also increases to match the longer objective
focal
length, manufacturers who use a parfocal distance of 45 millimeters are
at a
disadvantage in their inability to utilize the longer working distance
achieved by Nikon.
Using the Plan Apo 60x oil (N.A. 1.4) objective as a comparison, we see
W.D.s by
manufacturer to be at least 50 percent less than those of Nikon. This shows
that there
are differences in ability to accommodate various types of specimens as
well as ease
of operation.
Common Infinity Correction Tube Lengths
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Low power lenses demand a specific size. If the magnification of the objective
is 1x,
the "M(o) = F(t)/F(o)" formula used in the tube length section shows that
the focal
length of the objective and that of the tube lens would have to be the
same. In
Nikon's case, in order to perfect a tube lens focal length of 200 millimeters,
a parfocal
distance of 45 millimeters would leave too little space in the design.
By increasing this
distance to 60 millimeters, a magnification of 1x is obtainable and thanks
to this
revolutionary change, an objective with a magnification as low as 0.5x
has been
achieved. The lowest magnification offered by other manufacturers is 1.5x
and none of
them has produced a 1x objective yet.
Why Use a 25 millimeters Objective Thread Size?
When the focal length of the tube lens is increased, the focal length of
the objective
must also increase. There is a limit to the objective pupil diameter (effective
diameter
remaining after the limits of the objective thread size), so a high numerical
aperture
(N.A.) cannot be obtained. Thus, the N.A. of low-power lenses is critically
affected. At
present, other manufacturers use a 20.32 millimeters thread size, but as
mentioned
above, Nikon uses 25 millimeters and is able to attain high numerical apertures.
Originally, the brightness of photo lenses (F) was expressed with the formula:
F = f/D
where f is the lens focal length, and D is the effective diameter. Since
the N.A. of a
microscope corresponds to the F value of a photo lens, the brightness can
be
expressed with the formula:
F @ 1/(2N.A.)
The effective diameter needed to achieve a desired N.A. can thus be found
using this
formula. In other words, the size of the pupil on an objective (effective
diameter on the
exit side) is expressed as:
D = 2N.A. x f
For example, to find the effective diameter of the CFI Plan Apo 4x (N.A.
0.2), objective
with the highest (brightest) N.A.; given that the objective focal length
is 50 millimeters,
and where the focal length of the tube lens is 200 millimeters, the following
calculation
is made:
D = 2 x 0.2 x 50 = 20mm (optical diameter)
This shows that the conventional 20.32 thread size physically cannot be
used. Pupil
diameters required for designing 4x objectives with a numerical aperture
of 0.2 based
on 160 millimeters and 180 millimeters tube lengths are 16 millimeters
and 18
millimeters respectively. This shows the kind of design problems faced
by other
manufacturers when using a conventional 20.32 millimeters thread size.
The actual
numerical apertures of the respective Plan Apo 4x objectives are 0.16.
The N.A. for a
Nikon objective in this class is 0.20, which is the highest in the industry.
As shown, to obtain a high numerical aperture, a low-magnification objective
requires a
large pupil diameter. The longer the focal length of the tube lens, the
greater the
necessity to enlarge the thread size on the objective. Nikon has solved
this problem by
choosing a 25 millimeters thread size for the CFI Infinity Optics system.
In Conclusion
We trust these explanations accompanied by specific examples have helped
you to
understand why a tube lens of focal length 200 millimeters is considered
optimum for
use in an infinity optical system and why higher optical specifications
can be obtained
with an objective parfocal distance of 60 millimeters and a thread size
of 25
millimeters. Through JIS and other conventional standards have been followed
for
mechanical dimensions, the adoption of infinity optics itself has necessitated
a
sacrifice in compatibility with conventional systems.
Thus, rather than be bound by conventional dimensions, Nikon felt that
its true task
was to create products that users need for today's cutting edge microscopy
techniques. Innovations in engineering, manufacturing, quality control,
inspection, and
production, have all contributed to the advent of Nikon's CFI60 series
of optical
systems.
For more information, call Capra at (508) 650-9700.
